如何学好高中数学?
在立体几何的学习中,球心问题是很多同学的弱点;但是球心问题也是很热门的考点;其实在我看来这是因为同学们没有掌握正确的方法而已,本文介绍了一种找球心的方法,可以帮助同学们快速的解决找球心的相关问题。
有些同学在学习高中数学的时候都感觉比较吃力,有点跟不上老师的步伐,不知道如何学好高中数学?原因是高中数学相对于初中数学来说,难度层次更高,知识点,难点也更多,所以学习好高中数学,方法是关键。下面就和大家分享学霸们是怎么学好高中数学的。
如何学好高中数学,本质教育有三条重要的原则:
一,巩固基础知识,简单的题目做得又快又对;
二,学习数学三招,有逻辑地思考那些难题;
三,改掉错误习惯,避免运算错误、看错题目等毛病。
通过这篇文章,我们讲“到不在同一直线上的三点距离相等的集合定理”,来帮助基础知识掌握得不错的同学进一步提高解题速度,从而为我们学好高中数学走好第一步(文章尾部附有往期文章链接)
如何学好高中数学:提高解题速度定理-到不共线的三点距离相等的集合定理
到不在同一直线上的三点距离相等的集合是过三点形成的三角形的外心,并垂直于该面的直线。
附:该定理对于找球心的问题是很有帮助的
示意图:(直线l过外心O且垂直于平面ABC)
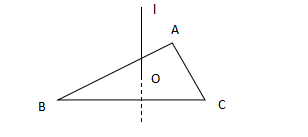
我们先证明一下这个公式:
在平面内到两定点距离相等的点的集合是线段的垂直平分线,那么我们升级到空间的尺度;在空间中到两定点距离相等的点的集合是线段的垂直平分面。
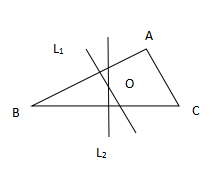
在下面给出的示意图中,到AB两点距离相等的点是AB的垂直平分线l1,到BC两点距离相等的点是BC的垂直平分线l2,两条垂直平分线的交点即为三角形ABC的外心。
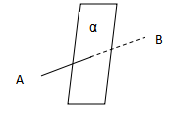
同样我们上升到空间中,因为到AB两定点距离相等的点的集合是线段AB的垂直平分面α,到BC两定点距离相等的点的集合是线段BC的垂直平分面β。由于两垂直平分面均垂直于底面,所以两垂直平分面的交线l也垂直于底面;由于在平面中两条垂直平分线的交点即为三角形ABC的外心,因此两面交线l在底面的投影点即是三角形ABC外心。
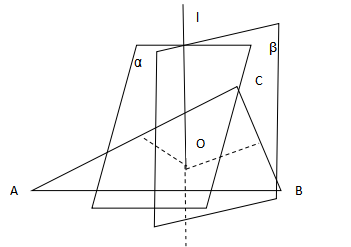
故两垂直平分面的交线l即为过ABC三点形成的三角形的外心,并垂直于该面的直线
从证明过程我们也可以发现,二级结论之所以为二级结论,就是很多时候它能帮助我们减少考试时遇到这类题目想办法去证明二级结论的时间,从而加快解题速度 。
如何学好高中数学:提高解题速度-实战演示
接下来,我们用一道例题来展示一下这个公式的简便性与实用性。
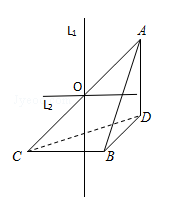
(2018春•南关区校级期末)如图,在四面体ABCD中,AD⊥平面BCD,BC⊥平面ABD,AD=BC=1,BD=,若该四面体的四个顶点均在球O的表面上,则球O的表面积为( )

【直接记住结论解题】
首先运用数学三招中的盯住目标,我们的目标是球的表面积,联想相关公式,我们的目标转化为求球的半径;再结合已知我们可以得出,我们要确定球心O的位置才能得出半径R
运用我们给出的定理,对于三角形BCD,到此三点距离相等的点的集合为过BCD三点形成的三角形的外心O1,并垂直于该面的直线。

如何学好高中数学:结论
通过上面的对比分析可以看出:
如果利用好这个公式,我们就能多一条翻译的路径,可简化很多繁琐的运算,即可迅速解出答案, 如果是在考试中就能大幅提高解题速度, 提高考试成绩, 学好高中数学
欢迎添加泽宇老师本人微信参加2小时的互动直播试听课。微信号:ZGSX02
也可以去了解全套录播课程: http://www.essence-edu.cn/courses

往期文章:

