数学题竟然还可以这样解之——角平分线定理1
你还在背方法学数学吗?
你还在题海战术中苦苦针扎但是成绩却提不高吗?
你是否也觉得书本上的知识点掌握的不错,但是考试却考不好?
这一些问题的原因就是你还没有形成正确的数学解题思维李泽宇三招TM。李泽宇三招TM,是一种哲学性的数学思维,分为翻译,特殊化,盯住目标,三个部分。
想了解更多的李泽宇三招TM内容吗?请继续看下去吧

大家看到李泽宇三招TM这个概念,是不是觉得比较抽象化呢?
那么通过这一个系列的文章,我们亲自示范如何使用李泽宇三招TM来解决高中和初中数学的各种题目,内容涵盖不同章节,不同难度的题目,从实例分析帮助同学们掌握李泽宇三招TM,从而帮助同学们学好数学,提高成绩。
李泽宇三招TM在初中角平分线题目中的应用-实战演示
首先,我们理解一下什么是角平分线定理
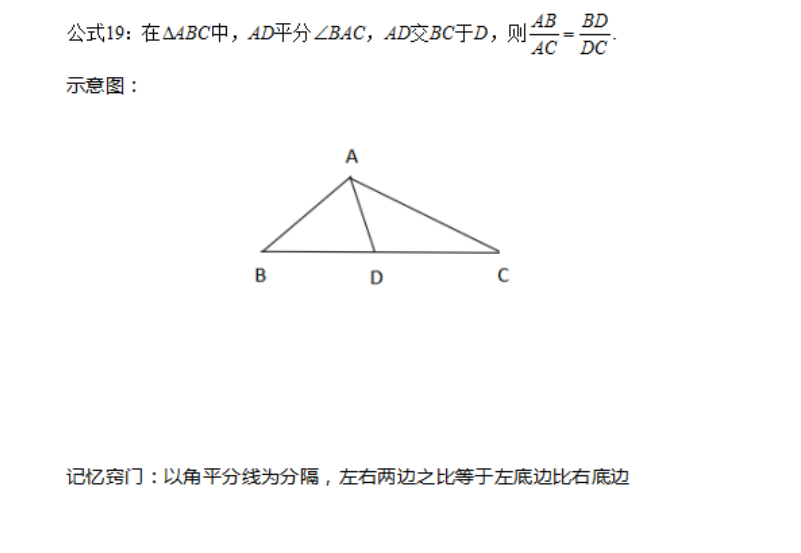
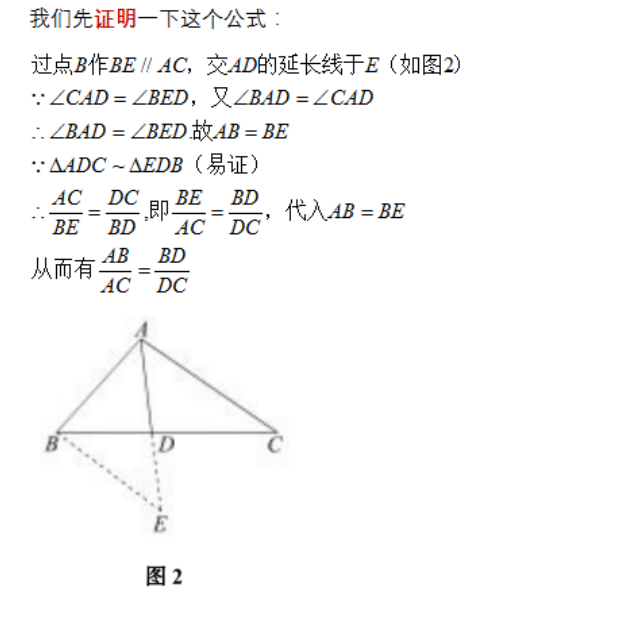
接下来,我们看一道中考真题
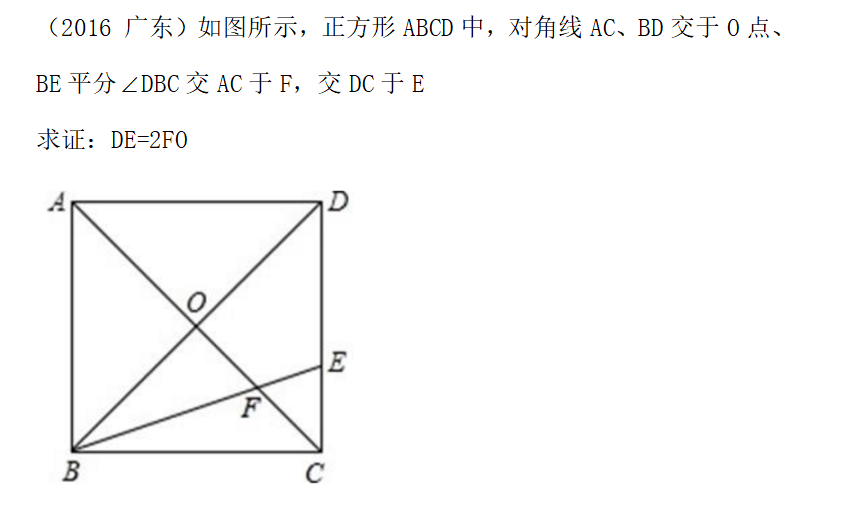


什么是数学思维-李泽宇三招TM?
本质教育李泽宇三招TM
- 翻译:
把中文翻译成为数学语言,包括:字母表示未知数、图像表示函数式或几何题目、概率语言等等。翻译要求“信、达、雅”不能扭曲原文的意思。该方法常用于函数,几何以及不等式等题目。
- 特殊化:
在面对抽象或者难以理解的题目的时候,我们尝试用最极端最特殊的数字来代替变量,帮助我们理解题目。该方法常用于在选择题目中排除选项,在解大题的过程中也经常会用到特殊化的结论。
- 盯住目标:
把目标和已知结合,联想相关的定理、定义、方法。在一些题目中,往往需要不断转化目标,即盯住目标需要反复使用!
大家掌握了吗?

学习李泽宇三招TM,是一个循序渐进的过程,需要大家自己在平时的考试和练习中应用三招。同时大家也可以观看本质教育的录播课程,体会用正确的数学思维做题时的感受。学会了正确的解题思维,考试的时候就会事半功倍!
欢迎添加泽宇老师本人微信参加2小时的互动直播试听课。微信号:ZGSX02
也可以去了解全套录播课程: http://www.essence-edu.cn/courses

往期文章:
1.你还在背题型?用数学思维高效解决高考数学难题——函数大题1

