如何学好高中数学-做到这几点你也可以成为立体几何的学霸

很多同学觉得立体几何很难，看到题目往往无从下手。而很多老师也宣称要学好立体几何需要具备所谓的“良好的空间想象能力”。看起来似乎很有道理，其实经不起推敲。在我看来，这种归因，说难听些，很有误人子弟之嫌。

如何学好高中数学：关于立体几何学习的误区

什么叫“良好的空间想象能力”，这本就是一个模糊的概念。用一个未界定清楚的概念去解释一种现象是极度不负责任的，这导致的后果就是很多学生潜意识会做出这样的推理：

1) 我的立体几何学不好->

2) 因为我没有良好的空间想象能力->

3) 良好的空间想象能力应该是天生的->

4) 因此我立体几何学不好是天生比别人在这方面“笨”->

5) 因此我再怎么努力也是徒劳的。

而很多老师教不得法，让那些努力学习了的孩子仍旧不能取得进步，于是，他们就更加相信上面的推理了，最终成为恶性循环。

在这里我想告诉这些努力了但没有收到效果的同学们一个好消息：不是你没有天分，而是你一直被错误地教导，你自己也在错误地归因，仅此而已。

事实上，你只要学好本质教育的三招中的第3招-盯住目标和第1招-翻译就可以解决高考难度的所有立体集合题目了。接下来，我用两道高考难度的例题带领大家学习下这两招，并说明如何灵活地运用他们。

如何学好高中数学：使用数学三招解决立体几何问题示例

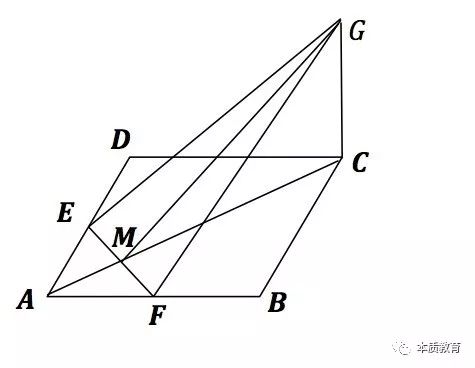
（我希望同学们在看我的分析前，先自己试着解答一下，看看你能否做出来，如果做出来了，看看能否一题多解。）

在我们开始分析之前，我们先来了解下本质教育数学第3招 – 盯住目标。事实上，任何解题的过程都是在已知（前提）和未知（结论）之间构建一个桥梁。我们把未知或者题目要证明的结论统称为目标(purpose)。解题的高手很清楚“有的放矢”这几个字， 我们往往不仅仅从已知出发正向构建桥梁，而是反过来从目标出发，反向构建桥梁：

在这个不断更新目标的过程中，我们反复问自己：盯住目标 – 你能联想相关的定理，方法，定义吗？你能试着把目标和已知，前提结合吗？这就是不断地调用学习过的知识的过程。

如何学好高中数学：数学三招在立体几何问题中的应用

这第三招这样看起来很抽象，我们通过例1来说明就会清楚多了：

我们利用第三招，从目标出发，问自己：盯住目标 – 你能联想相关的定理，方法，定义吗？

事实上，整个立体几何第一章空间的直线和平面的绝大多数定理可以用下图来总结：

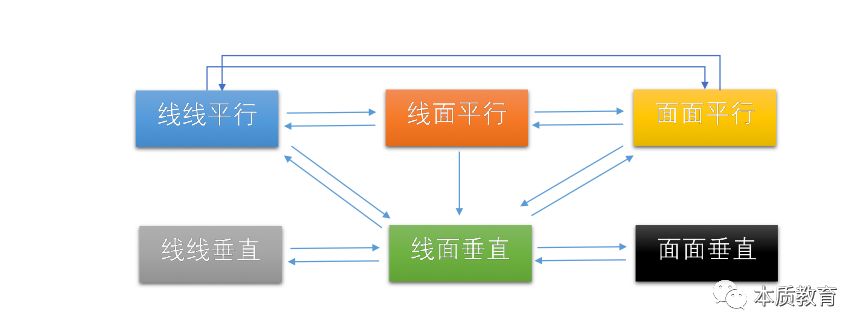
图1. 本质教育空间直线与平面定理总结图

换句话说，要证明线面垂直，我们应该根据此图联想出以下几个定理：

而联想出这3个定理，其实也对应着3种不同的证明方法：

当然你具体写出来的答案是反过来写的（这就是为什么很多时候你即使看懂了答案也不知道人家是如何想出来的）：

证法1：

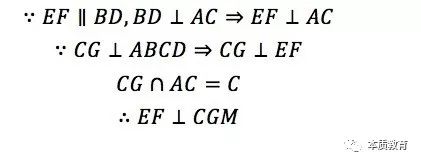
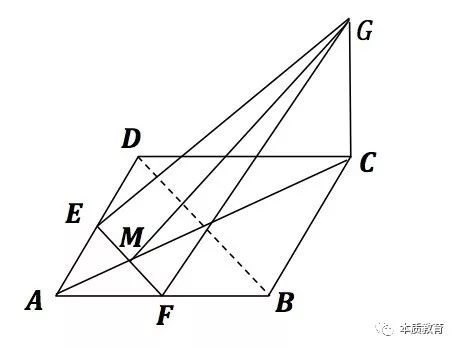
这就是第三招盯住目标的灵活性，我们从来没有规定你需要联想哪一个定理！而这题，联想不同的定理就出现了不同的证明方法。

我们接着看第二问：

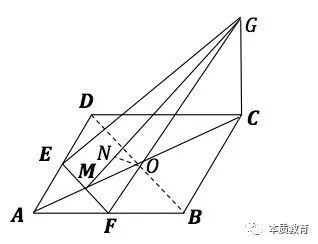
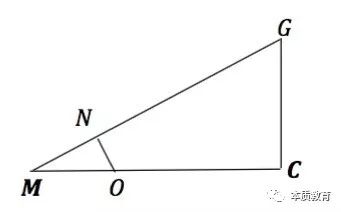
(还有别的解法吗？你能够联想不同的定理吗，你能够用另一种方法“翻译”这个问题吗？提示：空间向量)

回顾我的解题思路，用到了所谓的“空间想象力”了吗？完全没有！

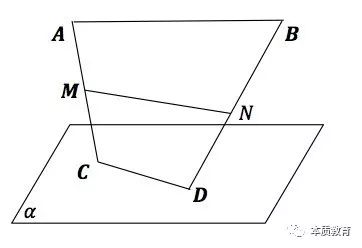
利用第三招-盯住目标，目标是证明线面平行，利用上图，我们可以联想以下两个定理：

（1）线线平行->线面平行：若一条平面外的直线和平面内的一条直线平行，那么该直线平行于这个平面

（2）面面平行->线面平行：若两个平面平行，那么其中一个平面内的任意一条直线平行于另一个平面

这也就形成了以下两个思路：

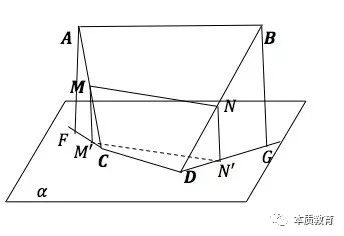
通过例2，同学们应该知道这些辅助线不是胡乱猜出来的，而是根据我们的第三招，有的放矢的找出来的！联想不同的定理，我们有不同的证明方法！我们用到了所谓的“空间想象力”了吗？还是没有。

如何学好高中数学：使用数学三招可以轻松解决压轴难度的立体几何题目

这两题就是高考所能考察立体几何的难度，我们不仅能做，还能够用多种方法求解，这就是我们本质教育三招的妙处，而这3招正是数学哲学的一部分，是一流数学家解决问题的思维方式。学习这三招就和游泳类似，你在岸上看我如何游泳是永远学不会如何游泳的，你必须下水，哪怕呛一两口水也好，这样才能知行合一，真正学会我们的三招，成为高中数学的学霸！

——本文为本质教育原创文章， 转载须经过本质教育同意，且注明出处！——